X-Ray Data Booklet

Section 3.1  SCATTERING of X-RAYS from ELECTRONS and ATOMS


Janos Kirz

    A. COHERENT, RAYLEIGH, OR ELASTIC SCATTERING

Scattering from single electrons (Thomson scattering) has a total cross section

                           (1)

where  is the classical radius of the electron,   meter. The angular distribution for unpolarized incident radiation is proportional to , where q is the scattering angle. For polarized incident radiation, the cross section vanishes at 90° in the plane of polarization.

Scattering from atoms involves the cooperative effect of all the electrons, and the cross section becomes

             (2)

where  is the (complex) atomic scattering factor, tabulated in Section 2.7 of this booklet. Up to about 2 keV, the scattering factor is approximately independent of scattering angle, with a real part that represents the effective number of electrons that participate in the scattering. At higher energies, the scattering factor falls off rapidly with scattering angle. For details see Ref. 1.

    B. COMPTON SCATTERING

In relativistic quantum mechanics, the scattering of x-rays by a free electron is given by the Klein-Nishina formula. If we assume unpolarized x-rays and unaligned electrons, this formula can be approximated as follows for x-ray energies below 100 keV:

                             (3)

where , the photon energy measured in units of the electron rest energy. The total cross section is approximately

                                   (4)

Note that for very low energies , we recover the Thomson cross section. The real difference comes when we deal with atoms. In that case, if the scattering leaves the atom in the ground state, we deal with coherent scattering (see above), whereas if the electron is ejected from the atoms, the scattering is (incoherent) Compton scattering. At high energies, the total Compton cross section approaches . At low energies and small scattering angles, however, binding effects are very important, the Compton cross section is significantly reduced, and coherent scattering dominates (see Figs. 3-1 and 3-2). For details see Refs. 1 and 2.

The scattered x-ray suffers an energy loss, which (ignoring binding effects) is given by

                                             (5)

or, in terms of the wavelength shift,

                                                (6)

where .  The kinetic energy of the recoil electron is just the energy lost by the photon in this approximation:

                                              (7)

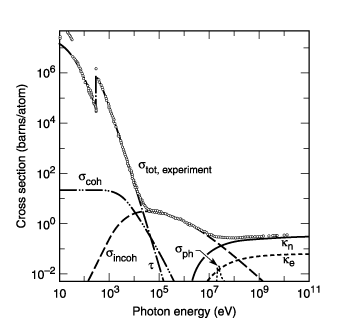
Fig. 3-1.    Total photon cross section  in carbon, as a function of energy, showing the contributions of different processes: t, atomic photo-effect (electron ejection, photon absorption); , coherent scat­tering (Rayleigh scattering—atom neither ionized nor excited); , incoherent scattering (Comp- ton scattering off an electron); , pair production, nuclear field; , pair production, electron field; , photonuclear absorption (nuclear absorption, usually followed by emission of a neutron or other particle). (From Ref. 3; figure courtesy of J. H. Hubbell.)

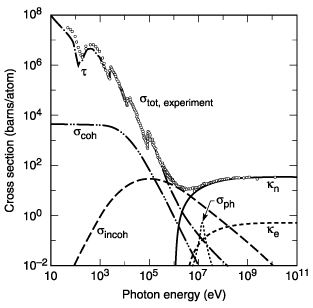
Fig. 3-2.    Total photon cross section  in lead, as a function of energy. See Fig. 3-1. (From Ref. 3; figure courtesy of J. H. Hubbell.)

REFERENCES

1.      J. H. Hubbell, W. J. Veigele, E. A. Briggs, R. T. Brown, D. T. Cromer, and R. J. Howerton, “Atomic Form Factors, Incoherent Scattering Functions, and Photon Scattering Cross Sections,” J. Phys. Chem. Ref. Data 4, 471 (1975).

2.      R. D. Evans, The Atomic Nucleus (Kreiger, Malabar, FL, 1982); R. D. Evans, “The Compton Effect,” in S. Flugge, Ed., Handbuch der Physik, vol. 34 (Springer-Verlag, Berlin, 1958), p. 218; W. J. Veigele, P. T. Tracy, and E. M. Henry, “Compton Effect and Electron Binding,” Am. J. Phys. 34, 1116 (1966).

3.      J. H. Hubbell, H. A. Gimm, I. , “Pair, Triplet, and Total Atomic Cross Sections (and Mass Attenuation Coefficients) for 1 MeV–100 GeV Photons in Elements Z = 1 to 100,” J. Phys. Chem. Ref. Data 9, 1023 (1980).